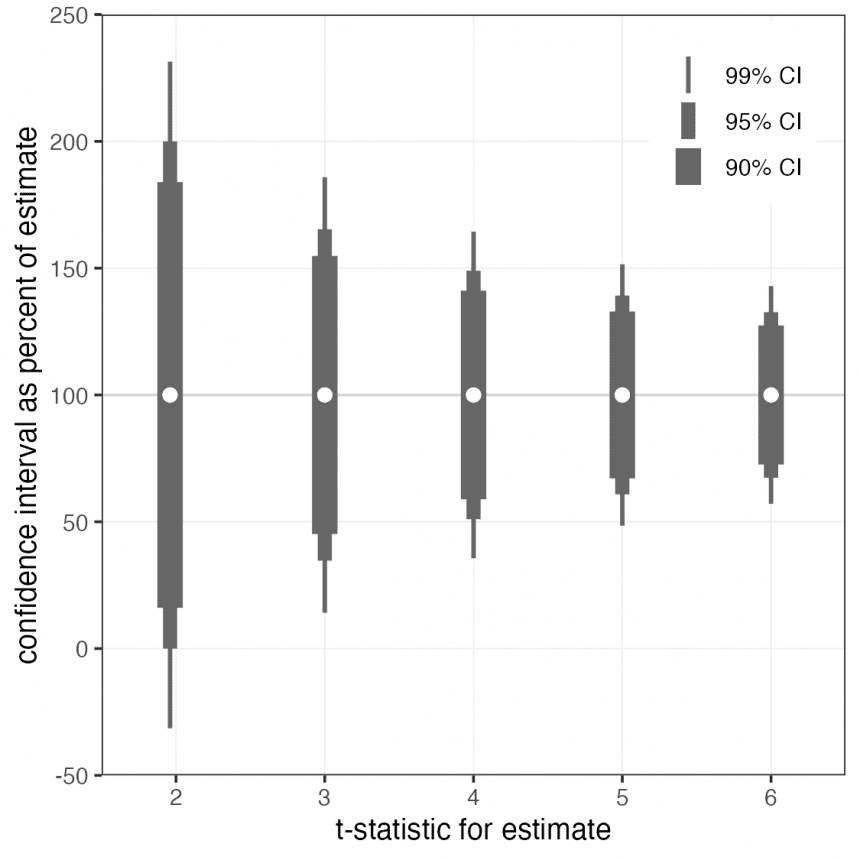
What does a statistically significant estimate tell you quantitatively? If you have an estimate that is statistically distinguishable from zero using the t statistic, what does that tell you about the confidence interval? Is it there?
Perhaps most simply, if the t-statistic is 2, the 95% confidence interval is close to 0. In other words, the confidence interval is exactly about 100% wide in each direction. Therefore, it covers everything from nothing (0%) to about twice the estimated value (200%).
More generally, for a 95% confidence interval (CI), 1.96/t (for example, 2/t) gives the relative half-width of the CI. Therefore, for the t=4 estimate, everything from half the estimate to 150% of the estimate is within the 95% CI.
For other commonly used nominal coverage rates, the width of the confidence interval is not very useful as a rule of thumb because the critical value is not as good as about 2. (For example, for a 99% CI, the Gaussian critical value is 2.58.) Let's look at the 90, 95, and 99% confidence intervals for t = 1.96, 3, 4, 5, and 6.
For example, you can see that even at t=5, the half-point estimate is still within the 99% CI. Perhaps this serves to emphasize how much higher precision is required to confidently express effect sizes than simply rejecting the null.
These „relative“ confidence intervals are just smooth functions of t (and thus the p-value), as shown here.
Relatively tight confidence intervals are obtained only when the statistical evidence against the null is overwhelming (more overwhelming than „six sigma“). This highlights that the default power analysis may be too optimistic, especially if estimates need to be used quantitatively rather than simply rejecting the null.
Note: All of this only considers standard confidence intervals based on normal theory labeled with nominal ranges. Of course, many of the estimates of p < 0.05 may have been arrived at precisely as a result of wandering through the garden of divergent paths or because they passed a statistical significance filter. In that case, these CIs will no longer receive conditionally advertised coverage.