Ole Folke writes:
I wanted to highlight paper This author has previously been featured on your blog when he was one of the co-authors of a paper on the impact of strip clubs on sex crimes in New York. This paper examines the impact of the criminalization of prostitution in Sweden and finds an increase of 40-60%. But this paper suffers from the same problems as the strip club paper. His main characteristics, which I think he has two, are that he uses the timing of the ban to assess its effectiveness. However, although there are no differences between regions, he uses regional data to estimate the effect, which of course makes no sense. Naturally, no adjustment is made for the dependence of the error term across observations.
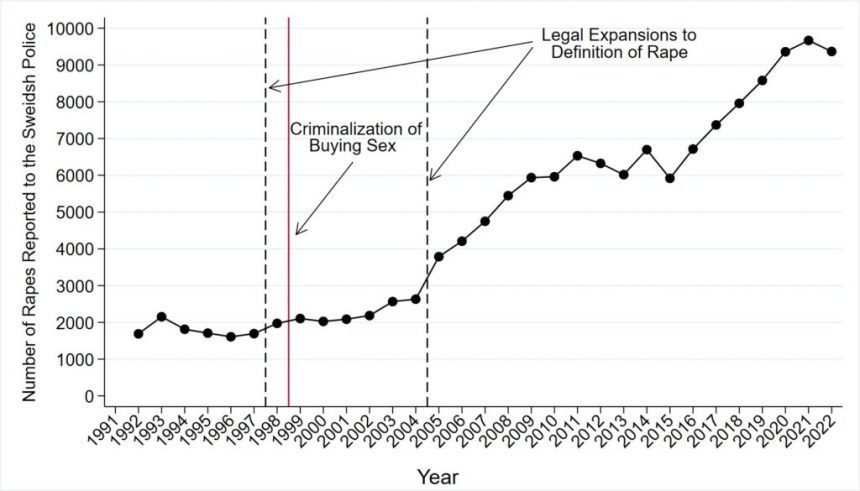
What's particularly odd about this analysis is that the results don't actually change when using national data (see the chart below). So basically the result must be what was created. The author hasn't posted any duplicate files, so we can't figure out what he did to achieve the large increase.
I think his answer to this criticism is that he has three alternative estimation methods. However, these are not very convincing, and I suspect that neither result is worthy of scrutiny. I also think using alternative techniques is strange and problematic. First, it suggests that neither method is persuasive in itself. However, running four more problematic analyzes does not improve the first one. Also, each analysis takes a lot of effort to perform (especially in the absence of replicate data), which puts authors at a disadvantage when criticized.

I looked at the linked paper and found that. . . Yes, I'm a skeptic. The article begins:
This paper leverages the timing of the sex trafficking ban to assess its impact on rape crimes. Based on Swedish high-frequency data from 1997 to 2014, we found that the ban increased the number of rapes by approximately 44-62%.
However, the above graph provided by Folke shows no obvious effect. The linked paper has a similar graph using monthly data, which also shows:
Nothing special happened in 1999.


This is a little hard to read due to the two axes, logarithmic scale, and short time frame, but the numbers look similar. For the period under study, the red curve is about 5.0 on a logarithmic scale per month, 12*log(5) = 1781, and the annual curve is about 2000, so they seem to match.
So overall not much is happening. But then the newspapers read:
Some evidence shows that rape more than doubled after the introduction of the ban. First, Table 1 shows that before the ban, the average was about 6 rapes per month by region, compared to about 12 after its introduction. Next, Table 2 shows the results of a naive analysis of rape regression on a binary variable with a pre-ban value of 0. We control for ban and subsequent year, month, and region fixed effects. Results show that the post-ban period is associated with an approximately 100% increase in log rape cases and a 125% increase in inverse hyperbolic sine transformation (IHS) rape cases. . Third, a simple descriptive exercise, by removing pre-treatment fixed effects, plots rape normalized to near zero before the ban, and finds that rape increases by about 110% over the sample period. (Figure 4).
OK, averages don't really tell us much. We're looking at data from 1997 to 2014, but the policy change occurred in 1999 during the middle of a slow increase, and most of the changes occurred after 2004. This is clearly shown in Folke's graph. Therefore, Tables 1 and 2 are largely unrelated.
But what about Figure 4?
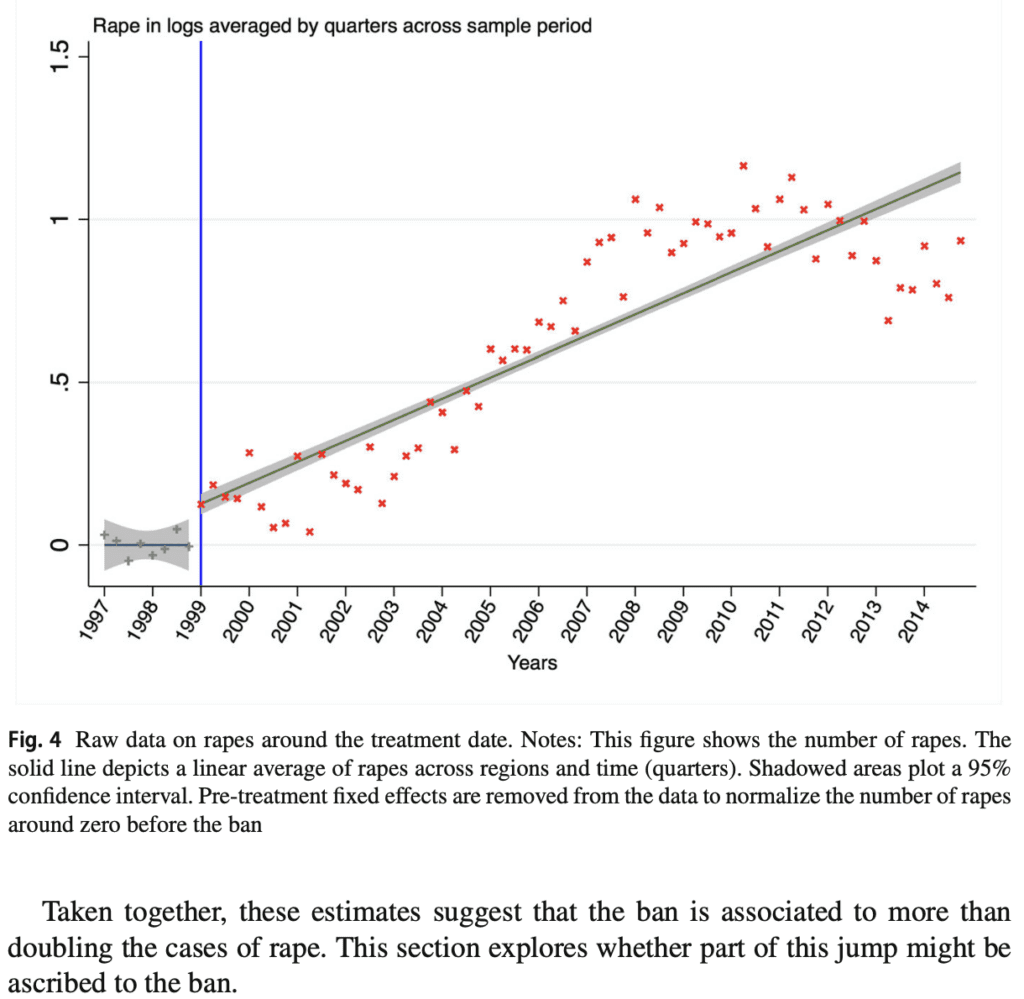

Doesn't this sound pretty convincing?
i dunno. First of all, the „more than double“ claim relies very heavily on his data from 2004 onwards. log(2) = 0.69, and if you look at that graph, the point is he only reached 0.69 around 2007, so the inference is: We place great emphasis on the model of steady annual increases with treatment, rather than short-term changes in levels at the time of treatment. Another issue is data from before 1999. This graph shows a flat line, but his two graphs earlier in this article show an increasing trend. This makes a big difference in Figure 4. If we replace the pre-1999 flat line with a line slanted to the right, the story looks very different. Indeed, the line is very flat and above zero, so this is due to the statistical fitting procedure (where pre-treatment fixed effects are removed from the data to normalize the pre-ban rape counts around zero). ”). ). I'm not sure. What matters is that something went wrong.
Next, we present a regression discontinuity model that fits changes in level rather than slope.


There's something else strange going on here. If they're actually fitting fixed effects across years, how can they estimate changes over time? This doesn't make much sense.
I am not going to review everything in this paper in detail. I just did the quick check above to get a rough idea of what's going on and to make sure there are no immediate problems with Folke's basic analysis. .
Folke continued:
The paper is even stranger than I expected. I got a piece of regression code, and he estimates a model that doesn't get an estimate for the treatment in the absence of coding errors (the treatment is constant within a few years, but fixed for a year effects). Also, when I run his RD analysis, which he claims to be doing, I get the figure below, which clearly doesn't show the 0.6 log point jump.


What the hell? ? ? ?
this is, Hall of regression discontinuities.
The next day, Folke followed up:
It took some digging and coding to understand how the authors were able to find such a large effect. We (Joop Adema, Olle Folke, Johanna Rickne) are now finished the draft In his comments, he indicated that it was all based on a misspecification, and he ended up estimating something completely different than what he was claiming.
The big picture, or how to avoid this type of error or reduce its impact?
Look, everyone makes mistakes. Statistical models are difficult to fit and interpret, data can be confusing, and social science theories are so vague that they can explain almost anything if you're not careful.
Still, the paper was an utter disaster, and a bit of an embarrassment for the Population Economics journal that published it.
Should we have noticed the problem sooner? I would argue so.
The problem with regression discontinuity models — well, you can't expect paper authors, reviewers, and editors to look at it carefully — it's a big, ugly equation, after all — and you can't expect authors to. It's a lot of work for reviewers and editors to check your code, right? A meaningless equation, it's just the cost of doing business.
An obvious problem is the pattern in the national time-series aggregate data, which does not show a spike in 1999.
I'm not saying that. Just because there wasn't a surge in 1999 doesn't mean the policy was ineffective. What I'm saying is that it's obvious to everyone that there was no jump in 1999. At the very least, if you claim to have discovered an effect, you have a scientific obligation to explain how you discovered it, given the lack of patterns in the aggregate data. Things like this happen. At the same time, other patterns may produce countervailing effects that happen to occur in the data. But in that case you need to explain it. breadcrumb trail.
So I'm not saying that the paper's authors, reviewers, or editors should have noticed all or even most of the paper's problems. What I'm saying is that they should have addressed the contradiction between their claims and what was shown in a simple timeline. Not doing this is a kind of „scientism“, a kind of mystical belief in the output of black boxes, a „trust the statistics, not the lying eyes“ kind of attitude.
Also, as Folke points out, the authors of this paper Achievements How to use questionable data analysis to extract dramatic discoveries.
There's no reason to think the author is doing anything wrong on purpose. Statistics is difficult! The authors' main mistakes in these two papers are:
1. Follow a workflow where objections are ignored or set aside rather than being directly addressed.
2. Lack of openness to the possibility that the work has fatal flaws.
3. Various technical errors, including insufficient concern for data quality, misunderstanding of regression discontinuity checks, and inappropriate belief in robustness checks.
In this case, Adema, Folke, and Rickne did a lot of work tracking down what went wrong in the published analysis. A lot of work for obscure papers in minor journals. But I share the story here because its results provide a useful general lesson.